Студентам > Дипломные работы > Анализ погрешностей волоконно-оптического гироскопа
Анализ погрешностей волоконно-оптического гироскопаСтраница: 6/11
На схеме
минимальной конфигурации ВОГ (рис.1.7.) показаны модуляторы М, которые при
необходимости могут быть включены в различные точки оптического гироскопа. Как
правило - это частотные и фазовые модуляторы, назначение которых состоит в
переносе фазы Саньяка на сигнал переменной частоты либо в частотной компенсации
этой фазы - с тем, чтобы измерения угловой скорости проводить на переменном
сигнале. Кроме того, модуляцией можно уменьшить шумы обратного рэлеевского
рассеяния.
В
качестве фотодетектора в практике конструирования ВОГ применяют фотодиоды (ФД),
р - i - n -фотодиоды и лавинные фотодиоды (ЛФД). Мощность лазерного источника
достаточна высока с тем, чтобы можно было использовать р - i - n -фотодиоды;
однако при применении СЛД могут потребоваться лавинные фотодиоды с внутренним
умножением. В последнем случае появляется дополнительный источник шумов -
случайные флуктуации коэффициента лавинного умножения.
2. Влияние элементов ВОГ на точностные
характеристики
системы
2.1. Характеристики
источников излучения для ВОГ.
При
конструировании волоконных оптических гироскопов, как правило, в качестве
излучателей используют полупроводниковые лазеры (лазерные диоды ЛД), светодиоды
(СД) и суперлюминесцентные диоды (СЛД). В ряде экспериментальных установок ВОГ,
однако, применяют также гелий-неоновые оптические квантовые генераторы. Их использование
объясняется, по-видимому, традиционным мнением о том, что в оптике при
измерении фазовых соотношений предпочтительны высококогерентные источники
излучений. При использовании гелий-неоновых ОКГ его излучение можно
«декогерировать» частотной модуляцией, что уменьшит влияние обратного
когерентного рэлеевского рассеяния, вносящего ошибку при измерении угловой
скорости вращения. Более того, для компенсации эффекта Керра, также вносящего
ошибку, можно применять широкополосные источники, приближающиеся по своим
спектральным свойствам к тепловым источникам.
Кроме
того, специфика конструкции ВОГ предъявляет дополнительные требования к
источникам излучения. К ним относят: соответствие длины волны излучения
номинальной длине волны световода, где потери минимальны; обеспечение
достаточно высокой эффективности ввода излучения в световод; возможность работы
источника излучения в непрерывном режиме без охлаждения; достаточно высокий
уровень выходной мощности излучателя; долговечность, воспроизводимость
характеристик, жесткость конструкции, а также минимальные габариты, масса,
потребляемая мощность и стоимость.
Наиболее
полно этим условиям отвечают полупроводниковые излучатели - ЛД, СД и СЛД.
Рассмотрим некоторые характеристики излучателей.
Возможность
использования полупроводниковых инжекционных лазеров в качестве источника
излучения в ВОГ привлекает исследователей и конструкторов прежде всего их
малыми габаритами и массой, высоким КПД, прямой токовой накачкой, твердотельной
конструкцией и низкой стоимостью. Кроме того, вводя различные примеси, можно
перекрывать требуемый диапазон длин волн.
В
настоящее время создано большое количество типов полупроводниковых инжекционных
лазеров или лазерных диодов (ЛД) на различных материалах. Принцип генерации
излучения ЛД имеет ряд существенных отличий от принципа генерации лазеров
других типов, что прежде всего связано с особенностями их энергетической структуры.
Рассмотрим
в общих чертах технические параметры ЛД, что позволит нам оценить возможность
использования тех или иных структур в волоконно-оптических гироскопах с учётом
требований налагаемых на них.
В
беспримесном полупроводнике различают следующие энергетические зоны: валентную,
запрещенную и зону проводимости. В реальном полупроводнике нужно учитывать
наличие примесей. Примеси являются причиной возникновения дополнительных
энергетических уровней. Донорные примеси создают уровни вблизи зоны
проводимости, а сами частицы примеси, ионизируясь, добавляют в возбужденную
зону (зону проводимости) избыточные электроны. Акцепторные примеси имеют уровни
вблизи валентной зоны. Эти примеси захватывают электроны из валентной зоны,
образуя в ней избыточное количество дырок. Число электронов в зоне проводимости
существенно превышает число дырок в валентной зоне (это характерно для
полупроводника n-типа, для полупроводника р-типа наоборот).
При
соединении полупроводников разных типов проводимости на границе их раздела
образуется р-n-переход.
Характер
распределения электронов по возможным энергетическим состояниям в
полупроводнике зависит от концентрации легирующей примеси и температуры. Для
того чтобы создать в полупроводнике условия генерации индуцированного
излучения, нужно нарушить равновесное распределение по энергетическим уровням,
т. е. перераспределить их так, чтобы на более высоких уровнях оказалось больше
электронов, чем на нижних. В полупроводниковых материалах возможны различные
переходы, электронов, такие как «зона—зона», «зона—примесь», и переходы между
уровнями примеси. Переход электрона на
более высокие
энергетические уровни сопровождается поглощением энергии извне. При переходе на
более низкие уровни энергия выделяется. При этом выделяющаяся энергия
излучается в виде электромагнитных колебаний, либо расходуется на нагрев
кристаллической решетки.
Для
перехода «зона—зона» инверсия населенности энергетических уровней имеет
место, если число электронов в зоне проводимости больше, чем в валентной зоне.
Инверсию населенности в полупроводниковых материалах можно реализовать лишь
путем создания неравновесной концентрации электронов и дырок.
Основным
способом создания инверсной населенности в полупроводниках является способ
инжекции через р - п- переход неравновесных носителей тока. Такая инжекция реализуется
подачей электрического смещения на р—п-переход в положительном направлении.
Тогда потенциал на границе раздела полупроводников снижается и через
переход начинает
протекать ток основных носителей дырок из р-области и электронов из n-области.
Зона с инверсной населенностью возникает вблизи р - n-перехода. При переходах
электронов из зоны проводимости в валентную зону возникает индуцированное
излучение, т. е. процесс индуцированного перехода сопровождается излучательной
рекомбинацией электронов и дырок в р - n -переходе. При излучательной
рекомбинации выделяется избыточная энергия в виде светового кванта.
Эффект
лазерной генерации света в полупроводниковых структурах возможен лишь при
наличии положительной обратной связи по световому излучению; при этом усиление
должно компенсировать оптические потери. Положительную обратную связь
осуществляет оптический резонатор Фабри — Перо, образованный отражающими
плоскопараллельными гранями кристалла, перпендикулярными плоскости р - n
-перехода. Отражающие поверхности создаются путем полировки двух
противоположных граней кристалла или путем скалывания по кристаллографическим
плоскостям. Коэффициент отражения этих поверхностей составляет приблизительно
0,3. Однако даже при небольшой длине активного вещества (десятые доли
миллиметра) такой коэффициент отражения достаточен для лазерной генерации
благодаря большому коэффициенту усиления активной среды.
В
настоящее время эффект вынужденной генерации получен на многих
полупроводниковых материалах; почти перекрыт диапазон генерации от 0,33 до 31
мкм.
Одна из
ранних конструкций инжекционного полупроводникового лазера была создана на
материале GaAs. В лазерном диоде нижняя пластина состоит из GaAs с примесью
теллура и имеет проводимость n-типа. Верхняя пластина состоит из GaAs с
примесью цинка и имеет проводимость р-типа. Каждая пластина имеет контакт для
соединения с источником питания. Геометрические размеры р - n -перехода
составляют сотые доли миллиметра, толщина области, в которой создается
излучение, 0,15...0,2 мкм. Торцевые отполированные грани образуют резонатор.
Излучатель такого типа работает в импульсном режиме при достаточно глубоком
охлаждении (77 К).
Для
GaAs-лазеров с простым р - n-переходом пороговые плотности тока при комнатной
температуре составляют значения > 105 А/см2. В таком режиме
полупроводниковый лазер нагревается настолько сильно, что без хорошего
теплоотвода длительная эксплуатация его иевозможия. Поэтому без охлаждения
такие GaAs-лазеры работают только в импульсном режиме. Длительная эксплуатация излучателя
при комнатной температуре (что важно для ВОГ) возможна лишь при уменьшении
пороговой плотности тока примерно до 103 А/см2.
Требованиям низких
пороговых плотностей тока и возможности длительной работы при комнатной
температуре отвечают полупроводниковые лазеры на двойных гетероструктурах
AIGaAs/GaAs. Они обладают еще целым рядом преимуществ, особенно важных при
конструировании ВОГ.
В
лазерах на структурах с двойными гетеропереходами уменьшается толщина активной
области рекомбинации, обеспечивается удержание носителей и излучения в узкой
области вблизи р - n -перехода. Это позволяет повысить КПД и создавать лазеры с
заданной диаграммой направленности излучения. В режиме индуцированной генерации
в двойной гетероструктуре затухание основной волны весьма мало, поскольку
структура образует диэлектрический волновод.
При
конструировании ВОГ в качестве излучателя, соединяемого с волоконным
световодом, применяют полупроводниковые лазеры с полосковой геометрией контакта
на двойных гетероструктурах. В таких конструкциях лазерное излучение выходит из
малой области, что обеспечивает хорошие условия ввода излучения в световоды с
низкой числовой апертурой. Из-за небольших размеров активной области лазер
обладает малыми пороговыми и рабочими токами при достаточной выходной мощности,
что обеспечивает длительную работу в непрерывном режиме при комнатной
температуре. При малом размере активной
области проще
получить площадь, свободную от дефектов, что важно для повышения эффективности
лазера.
Типичные
параметры полупроводниковых лазеров с двойной гетероструктурой, генерирующих в
области 0.8 - 0.9 мкм, следующие: ширина линии генерации 0.2 - 5 нм, размеры
излучающей области 0.5...30 мкм2 , средняя угловая
расходимость излучения 5... 30° (в плоскости, параллельной р - n -переходу) и
30 ... 60° (в плоскости, перпендикулярной р - n -переходу), выходная мощность 1
... 10 мВт, пороговый ток 20...200 мА, средняя долговечность 105 ч.
Современное
состояние технологии изготовления кварцевых оптических световодов позволило
создать световоды, имеющие минимум потерь и дисперсии в диапазоне длин волн 1,1
... 1,7 мкм. Этот диапазон рекомендуется использовать также и разработчикам
ВОГ. Эти потребности стимулировали разработку полупроводниковых лазеров на
данный диапазон длин волн. Полупроводниковым материалом послужили тройные и
четверные соединения. Были созданы полупроводниковые лазеры на гетероструктуре
GalnAsP/lnP, излучающие на длинах воли 1,3 и 1,6 мкм. Появились сообщения о
создании лазеров с гетероструктурами на основе соединений AIGaAsSb/GaAsSb,
генерирующих на длинах волн 1,3 мкм и 1,5... 1,6 мкм.
При
этом конструкции и параметры этих лазеров аналогичны конструкциям лазеров на
AIGaAs.
Светодиоды
(СД) генерируют некогерентное излучение, поскольку в них излучательная
рекомбинация носит чисто спонтанный характер. Спектральное распределение линии
излучения излучательной рекомбинации по крайней мере на порядок шире линии
излучения лазерных диодов. Широкий спектр излучения СД весьма благоприятен
для ВОГ, поскольку, за счет малой длины когерентности позволяет компенсировать
влияние эффекта Керра и обратного рэлеевского рассеяния.
Коэффициент
ввода излучения светодиодов в световоды с низкой числовой апертурой значительно
меньше, чем для лазерных диодов. Однако СД проще в конструктивном выполнении и
обладает меньшей температурной зависимостью мощности излучения. Так, в
частности, выходная мощность СД с двойным гетеропереходом уменьшается лишь в
два раза при увеличении температуры диода от комнатной до 100° С.
Возбуждение
СД обеспечивается инжекцией носителей через р - n -переход. Как и обычный
полупроводниковый лазер, простой СД содержит один р - n -переход в прямозонном
полупроводнике, лишь часть инжектированных электронов рекомбинируют
излучательно. Остальные теряются на безызлучательных рекомбинациях.
Уменьшить
рекомбинационные и оптические потери СД можно, если выполнить прибор с
гетеропереходами или даже на двойных гетероструктурах.
СД с
двойным гетеропереходом, разработан специально для соединения с волоконным
световодом. Область рекомбинации расположена вблизи хладопровода, а в
подложке из GaAs протравлена ямка, в которую вставляется световод.
Конструируются светодиоды как с выводом излучения через поверхность,
ограничивающую переход сверху (плоскостные СД), так и с выводом энергии в
направлении, параллельном плоскости р - n -перехода (торцевые СД). При этом
выходная мощность составляет несколько милливатт при плотностях тока около 103А/см . Так СД
изготовленный на основе AlGaAs-структуры с полосковым контактом шириной
100 мкм при плотности тока накачки 2 103 , имеет мощность
излучения 3 мВт на длине волны 0,8 мкм; СД с вытравленной ямкой и линзообразной
поверхностью имеет мощность излучения 6 мВт при плотности тока 3400 А/см.
Светодиоды
даже при высоких плотностях тока инжекции (свыше 10 А/см) оказываются очень
надежными; их средняя долговечность достигает 105 ...106 ч.
Широкое
применение получили суперлюминесцентные диоды. Как уже отмечалось,
излучательная рекомбинация в обычных светодиодах приводит к спонтанному
испусканию света. Это спонтанное излучение вызывает последующие излучательные
переходы и усиливает само себя (поскольку концентрация электронов и дырок не
является равновесной). Это усиление невелико, поскольку излучение проходит
тонкую область рекомбинации в поперечном направлении. Для получения лазерного
эффекта нужно это излучение направить вдоль активного слоя и обеспечить отражение
от концевых плоскостей. Однако усиление спонтанного излучения в такой
конфигурации наблюдается и ниже порога возбуждения и при неотражающих концевых
плоскостях. Усиленное и направленное таким образом испускание называется
суперлюминесценцией. На этом эффекте и основаны супсрлюминесцентиые диоды
(СЛД). При этом активную среду формируют в виде оптического волновода, который
замыкается на одном конце хорошо отражающим зеркалом, а на другом конце
излучает свет без отражения в пространство либо в световод. Для сильной
суперлюминесценции необходимо высокое усиление в активной среде, что в
полупроводниках обеспечивается высокой плотностью мощности. Суперлюминесцентные
диоды конструируются на основе двойной гетероструктуры с полосковой
геометрией. Контактные полоски с одной стороны доходят до торцевой фронтальной
поверхности, в то время как с другой стороны они не доходят до края
полупроводника. Именно на этой стороне суперлюминесценция затухает, поскольку в
эту область электроны не инжектируются. С фронтальной стороны генерируется
суперлюминесценция, при этом раскрыв диаграммы излучения определяется шириной и
длиной полоски.
При
конструировании двойной гетероструктуры с полосковой геометрией для СЛД
активная р-область GaAs делается толщиной 0,3 ... 0,5 мкм, контактная полоска
- шириной 12... 15 мкм. При длине полоски до 1,5 мм и плотности тока 104 А/см мощность
излучения в импульсном режиме достигает 50 мВт при ширине линии генерации 0,008
мкм.
2.2. Шумовые характеристики волоконно-оптического
контура
В оптической
гироскопии для намотки чувствительного контура используют три вида волокна:
многомодовое, одномодовое и одномодовое с устойчивой поляризацией. Длина
периметра контура определяется исходя из двух предпосылок. С одной стороны,
увеличение длины контура повышает точность системы в целом, так как величина
невзаимного фазового сдвига пропорциональна длине волокна, с другой стороны для
более длинного контура в большей степени на работу системы оказывают влияние параметры
затухания и нерегулярности волокна. Системы, где требуется высокая
чувствительность к низким скоростям вращения подразумевают выбор оптимальной
длины контура с учетом всех возможных факторов влияющих на точностные
характеристики системы. Обычно используются волокна длиной от 200 до 1500 м.
Диаметр
катушки выбирается по критерию минимизации потерь в волокне на изгибах и с
учетом габаритных размеров устройства. Типовое значение от 6 до 40 см.
В
зависимости от числа распространяющихся на рабочей частоте волн (мод) могут
использоваться одно- и многомодовые световоды.
Для
характеристик световода важное значение имеет профиль показателя преломления в
поперечном сечении. Используя возможности неоднородных световодов в широких
пределах изменять свои характеристики в зависимости от закона изменения
диэлектрической проницаемости по поперечному сечению, можно для каждого
конкретного применения подобрать световод с наилучшим соответствием его
характеристик решению задачи.
Важной
характеристикой световода является числовая апертура NA, представляющая
собой синус максимального угла падения лучей на торец световода, при котором в
световоде луч на границу «сердцевина-оболочка» падает под критическим углом. От значения NA зависят эффективность
ввода излучения светодиода в световод, потери на микроизгибах, дисперсия
импульсов, число распространяющихся мод.
В
практике волоконно-оптической гироскопии важно иметь оценочные характеристики
волокон различной структуры, не прибегая к сложным расчетам представлять общую
модель ошибок, которые могут заметно снизить точностные характеристики
системы. Получим приближенные соотношения для статистических характеристик
потерь в волокнах с различными свойствами и структурой определяющей их. Так как
многомодовые световоды имеют дисперсионные характеристики, сильно
ограничивающие точность приборов остановимся на рассмотрении одномодовых
волокон в составе общей теории распространения волн.
Рассмотрим
механизм потерь мощности в одномодовом волоконном световоде. При
распространении электромагнитной энергии вдоль нерегулярного световода часть
световой мощности рассеивается. Часть рассеивающейся мощности
перераспределяется между вперед и назад распространяющимися модами, а остальная
часть излучается. Интерес представляет вывод выражений для определения
численной оценки величины рассеивающейся мощности для волокон с известными
характеристиками профиля показателя преломления и допусковыми значениями
нерегулярностей.
Неоднородности
нерегулярных световодов удобно представлять как источники вынужденных токов,
находящихся внутри регулярного световода. При этом может быть описано возбуждение
как направленных мод, так и поля излучения.
Нерегулярности
световодов приводят к зависимости показателя преломления от продольной
координаты, т.е. n=n(x,y,z). Полные электрическое и магнитное поля
E
(x,y,z) и H(x,y,z) в любой точке внутри нерегулярного световода связаны между
собой уравнениями Максвелла для среды без источников. С другой стороны, эти
поля можно представить в виде поля регулярного световода, в котором имеются
источники тока :
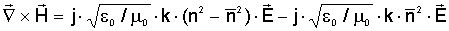 (2.1) (2.1)
Здесь 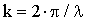 - волновое число в
свободном пространстве; - волновое число в
свободном пространстве;
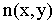 - профиль того же
световода без неоднородностей. - профиль того же
световода без неоднородностей.
Величину
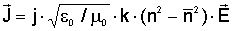 (2.2) (2.2)
называют
вынужденной плотностью тока, обусловленной неоднородностью. Источник
вынужденного тока (2.2) существует только внутри области неоднородности и
целиком определен при условии известности полного электрического поля Е. Если
световод является слабонаправляющим и n » n, то поля мод
являются приблизительно поперечными и в первом приближении можно считать, что E = Ex ,
а
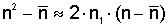 (2.3) (2.3)
Индекс x означает
поперечную компоненту поля, а n1 - показатель преломления сердцевины
волокна, иначе n(a)= n1 при а<r, где
r - радиус сердцевины
волокна.
Таким
образом из (2.2) и (2.3) имеем:
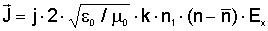 (2.4)
(2.4)
В этом
приближении не учтены все поляризационные эффекты, обусловленные
неоднородностями, поскольку в рамках приближения слабонаправляющего световода
поперечные поля всех мод ортогональны друг другу. В частности, поляризованная
вдоль оси x чётная основная мода не может быть возбуждена нечётной или
поляризованной вдоль оси y основной модой.
Подставив
в (2.4) выражение для электрического поля в гауссовом приближении рассмотренном
в [1], получим следующее выражение для плотности тока, если на
неоднородность в круглом световоде падает основная мода, поляризованная вдоль
оси x :
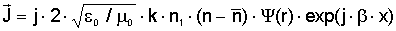 ,
(2.5) ,
(2.5)
где 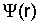 - фундаментальное
решение скалярного волнового уравнения для поля основной моды, определяемой в
зависимости от профиля показателя преломления . - фундаментальное
решение скалярного волнового уравнения для поля основной моды, определяемой в
зависимости от профиля показателя преломления .
Вследствие
того что, волоконные световоды, используемые в волоконной гироскопии, являются
слабонаправляющими, т.е. относительная разность между максимальным и
минимальным значениями профиля показателя преломления n ( r ) мала, векторы Е и
H аппроксимируются
решениями скалярного волнового уравнения. Постоянная распространения b основной моды,
направляемой по световоду, ограничивается интервалом между двумя экстремумами,
которые определяются значениями b для плоских волн. В бесконечных средах с
показателями преломления n1 и n2 :
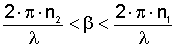 ,
(2.6) ,
(2.6)
где n1 , n2 - максимальное
и минимальное значения показателя преломления n (
r ); 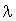 - длина волны в вакууме. - длина волны в вакууме.
В силу
слабой канализации волн в световодах, т.е. n1 »n2 из (2.6) следует b » 2 p
n / l, что совпадает с
постоянной распространения плоской волны в направлении Z в бесконечной
среде с показателем преломления n2 £ n £ n1 .
Таким
образом, основная мода волоконного световода является квазипоперечной
электромагнитной (Т) волной. В простейшем случае - это волна, однородно
поляризованная только в одном направлении в отличии от мод высших порядков.
Если обозначить направление поляризации через Х, поле в световоде можно представить
в виде
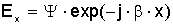
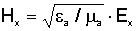 , (2.7) , (2.7)
где 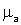 - магнитная проницаемость среды; - магнитная проницаемость среды;
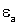 = = 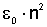 - диэлектрическая проницаемость среды; - диэлектрическая проницаемость среды;
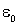 - диэлектрическая
проницаемость вакуума. - диэлектрическая
проницаемость вакуума.
Здесь
неявно подразумеваем временную зависимость 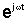 . Компоненты поля
Ey ,
Ez , Hx , Hz не учитываются поскольку они
пренебрежимо малы, Y описывает пространственное изменение поля в плоскости,
перпендикулярной оси световода. Следует отметить, что отражение плоской волны
от границы раздела диэлектрических сред с близкими параметрами практически не
чувствительно к поляризации падающей волны. Соответственно, и пространственное
изменение поля Y должно быть нечувствительно к поляризационным эффектам,
поэтому Y - решение
скалярного волнового уравнения, т.е. . Компоненты поля
Ey ,
Ez , Hx , Hz не учитываются поскольку они
пренебрежимо малы, Y описывает пространственное изменение поля в плоскости,
перпендикулярной оси световода. Следует отметить, что отражение плоской волны
от границы раздела диэлектрических сред с близкими параметрами практически не
чувствительно к поляризации падающей волны. Соответственно, и пространственное
изменение поля Y должно быть нечувствительно к поляризационным эффектам,
поэтому Y - решение
скалярного волнового уравнения, т.е.
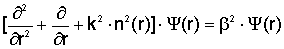 ,
(2.8) ,
(2.8)
где:
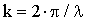
n ( r ) - профиль показателя преломления; l - длина волны в
вакууме.
Таким
образом, основная мода описывается решением уравнения (2.8), соответствующим
наибольшему b и 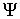 , не зависящей от
угла , не зависящей от
угла 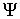 . Для регулярного световода
n ( r ) не зависит от
длины, в случае нерегулярного световода n=n(x,y,z). . Для регулярного световода
n ( r ) не зависит от
длины, в случае нерегулярного световода n=n(x,y,z).
В
практически интересных случаях применяют в одномодовых световодах оптические
волокна как со ступенчатым, так и градиентным профилем. При этом наибольшее
распространение получили оптические волокна с гауссовым и ступенчатым
профилями. Эти волокна целесообразно применять и в волоконной гироскопии
поэтому остановимся на их анализе подробнее.
При
изготовлении световодов в следствии диффузии границы между оболочкой и
сердцевиной реальные профили могут отличаться как от ступенчатого, так и от
гауссова, занимая некоторое промежуточное положение (сглаженный ступенчатый
профиль). При этом профиль показателя преломления представляют в виде :
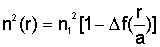 (2.9)
(2.9)
где 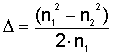 - параметр высоты профиля. - параметр высоты профиля.
Численные
решения волнового уравнения для ступенчатого и степенного профилей волокна
[2] показывают, что форма Y (r) примерно гауссова.
В соответствии с этими исследованиями поле моды HE11 можно представить
в виде:
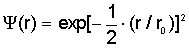 (2.10) (2.10)
где r0 -
размер
светового пятна, определенный вариационным методом в
[2].
Для
решения волнового уравнения умножим его на 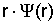
и воспользуемся
тождеством:
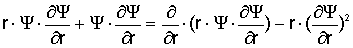 (2.11)
(2.11)
После
интегрирования в пределах от 0 до ¥ получаем
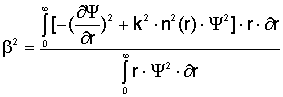 (2.12) (2.12)
Кроме
(2.12) появляется дополнительный член 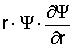 , ,
который вычисляется
при значениях r = 0 и ¥. Этот член равен нулю, поскольку 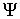 конечно при r = 0 и экспоненциально
стремиться к нулю при r ® ¥. конечно при r = 0 и экспоненциально
стремиться к нулю при r ® ¥.
Размер
пятна r0 выбирается из
условия обеспечения наибольшего b, которое соответствует основной моде.
Подставляя приближенное выражение (2.10) в (2.12), можно определить
r0 из условия db2/ dr0
= 0.
Приближение для постоянной распространения b получается далее подстановкой найденного
r0
в
выражение (2.12). Таким образом, зная r0 и b можно полностью
характеризовать поле с помощью формул (2.7) и (2.10). Используем полученную
методику для определения параметров r0 и b для профилей
применяемых в волокнах для оптической гироскопии.
В
случае гауссова профиля показателя преломления:
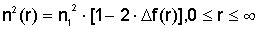 ,
(2.13) ,
(2.13)
где 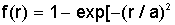 . .
Таким
образом, n(r) с ростом r от 0 до ¥ уменьшается плавно
от n1 до n2. Поскольку чёткой
границы между сердцевиной и оболочкой нет, то форму профиля
определяет радиус сердцевины a. Такая форма профиля показателя
преломления представляет практический интерес, так как является
хорошим приближением реального случая, когда в процессе изготовления волоконных
световодов происходит взаимная диффузия материала сердцевины и оболочки.
Подставляя
(2.13) в (2.10) и (2.12), из условия db2/dr0
= 0 находим
величину
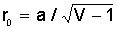 (2.14) (2.14)
Выражение (2.14)
имеет физический смысл только при V >>1 (r0 - положительно), однако это не
уменьшает его практической ценности, так как при
V £ 1 вблизи оси
световода распространяется лишь малая доля мощности основной моды. Подставляя
r0 в (2.12) получаем
выражение для
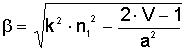 ,
(2.15) ,
(2.15)
где
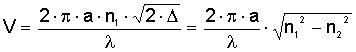 (2.16) (2.16)
Размер пятна
r0 и постоянная
распространения b полностью характеризуют поле основной моды, а следовательно, и передаточные
свойства одномодовых световодов.
Распределение
плотности мощности или профиль интенсивности S(r) имеет вид :
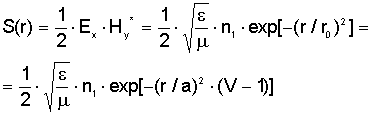 , (2.17) , (2.17)
где e,m - относительная
диэлектрическая и магнитная проницаемость вакуума.
С
увеличением расстояния от оси световода интенсивность падает экспоненциально.
При меньших значениях V спад происходит медленнее, поэтому чем меньше V, тем меньшая часть полной мощности распространяется вблизи оси волокна.
Доля мощности, распространяющейся в интервале от 0 до
r, равна
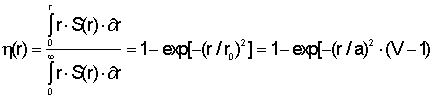 (2.18)
(2.18)
Таким
образом в световодах с малым V распространяющееся излучение захватывает
большую область поперечного сечения. Поскольку в практических ситуациях такое
положение нежелательно, ограничение на V >1 (2.14) не важно.
Практический интерес представляет определить ширину a профиля показателя
преломления, при которой мощность пучка света будет наиболее сильно
концентрироваться вблизи оси волокна при фиксированных значениях D и длины волны
излучения, т.е. определить значение радиуса сердцевины, обеспечивающего
минимальный размер пятна r0. Дифференцируя
(2.14) по a и учитывая, что согласно (2.16)
V пропорционально a, получим оптимальное
значение a, соответствующее V=2, т.е.
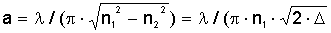 )
(2.19) )
(2.19)
При V = 2 имеем
r0
= a, т.е.
распределение интенсивности S(r) совпадает с формой профиля показателя
преломления.
В
случае световода
со ступенчатым профилем показателя преломления:
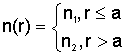 (2.20) (2.20)
( S =1, f
= 0 при r £ a и S =0, f =1 при
r >
a).
Следуя методике
определения r0 и b для световодов с гауссовым профилем, получаем
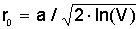 (2.21) (2.21)
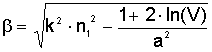 (2.22) (2.22)
Все
физические процессы имеющие место в волокнах с гауссовым профилем преломления, справедливы и для
волокна со ступенчатым профилем. Радиус сердцевины a, обеспечивающий
максимальную концентрацию света в волокне, определим в данном
случае из условия V = exp(1/2) » 1.65 что соответствует
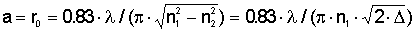 (2.23)
(2.23)
Таким образом, плотность мощности
в ступенчатом волоконном световоде выше на 17%. Доля мощности, распространяющейся
в пределах радиуса r, будет равна
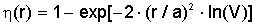 (2.24)
(2.24)
Получим основные
характеристики одномодовых световодов на основе выводов сделанных ранее.
Рассмотрим амплитуду излучения и мощность распространяющихся мод.
Для j - й вперёд и назад
распространяющихся мод полная мощность определяется соотношениями :
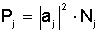 (2.25)
(2.25)
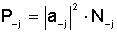 ,
(2.26) ,
(2.26)
где Nj ,
N-j - параметры нормировки.
Полная
мощность, возбуждённая во всех направляемых модах, будет равна
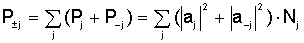 (2.27)
(2.27)
Если световод
является слабонаправляющим и круглым, а источники тока излучают вдоль оси
x поперечного
сечения световода, то мощность в каждой моде равна
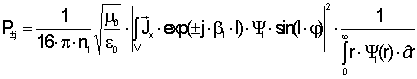 (2.28) (2.28)
где bl - скалярные
постоянные распространения;
Yl- решение скалярного
волнового уравнения (2.11).
Для определения
мощности излучения воспользуемся приближением свободного пространства, суть
которого сводится к замене слабонаправляющего световода неограниченной
однородной средой с показателем преломления оболочки n2 . В большинстве
практических случаях излученная мощность достаточно точно описывается в рамках
этого приближения.
Решение
уравнений Максвелла для полного поля в световоде с произвольным показателем
преломления, согласно методике, приведённой в [2], можно выразить
через векторный потенциал А, декартовы составляющие которого удовлетворяют уравнению
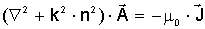 ,
(2.29) ,
(2.29)
где  - распределение
плотности тока; Ñ2 - скалярный оператор Лапласа. Решение
уравнения (2.29) для каждой составляющей выражается через функцию Грина в виде - распределение
плотности тока; Ñ2 - скалярный оператор Лапласа. Решение
уравнения (2.29) для каждой составляющей выражается через функцию Грина в виде
 ,
(2.30) ,
(2.30)
где V - объём, в котором
распределены источники тока;
 - радиусы-векторы
точки наблюдения поля и точки расположения источника соответственно (рис
2.1.а). - радиусы-векторы
точки наблюдения поля и точки расположения источника соответственно (рис
2.1.а).
Функция
Грина находится путём решения соответствующего уравнения для свободного
пространства с показателем преломления n2 и имеет вид
 , (2.31) , (2.31)
где  , а c - угол между векторами , а c - угол между векторами  и и  . .
Подстановка
(2.31) в (2.30) приводит к выражению
 , (2.32) , (2.32)
где


a)

б)
Рис 2.1. Возмущение поля
в точке P источником с плотностью тока J в точке
Q (а) и сферические
полярные координаты точек Р и Q (б).
Достаточно
далеко в оболочке поля всех источников являются локально плоскими и имеют вид
.
 (2.33) (2.33)
 (2.34) (2.34)
Отсюда
запишем полную мощность излучения в виде
 ,
(2.35) ,
(2.35)
 где с - скорость света; S¥ - сферическая
поверхность с радиусом ¥; W - пространственный угол; S = | r | - радиус среды; где с - скорость света; S¥ - сферическая
поверхность с радиусом ¥; W - пространственный угол; S = | r | - радиус среды; - единичный вектор,
параллельный радиальному вектору. - единичный вектор,
параллельный радиальному вектору.
Если
векторы P и Q выразить в сферической системе координат (S,Q,j) (рис 1.б), которая
ориентирована так, что если угол j равен нулю, радиус-вектор расположен в
плоскости Z, то уравнение (2.35) с использованием (2.32) и (2.33) можно
записать так
 , (2.36) , (2.36)
где Mq и Mj , q и j - составляющие
вектора  в
точке Р в
точке Р
В случае
поперечно-ориентированного источника (токи параллельны оси x) вектор  будет иметь только
составляющую Мх. Полную излученную мощность можно определить
подстановкой в (2.36): будет иметь только
составляющую Мх. Полную излученную мощность можно определить
подстановкой в (2.36):
 (2.37)
(2.37)
Здесь q0 - угол, под которым
происходит излучение источника к оси световода. Из рис 2.1.б следует, что
 ,
(2.38) ,
(2.38)
где a = S/
sin (q/) и z = S/
cos (q/) на трубке.
Подставляя (2.38) и
(2.37) в (2.33) получаем
 (2.39) (2.39)
Интеграл по j/ является
интегральным представлением функций Бесселя первого рода, нулевого порядка и
тогда
 , (2.40) , (2.40)
где J0(...) - функция Бесселя
первого рода нулевого порядка.
Запишем
величину плотности тока трубчатого источника (2.5) с учетом выражения
полученного в [2]
 (2.41)
(2.41)
где DS(r,z) - отклонение
функции профиля показателя преломления вследствие нерегулярностей.
 (2.42)
(2.42)
Подставив
(2.41) в (2.40) получим
  , (2.43) , (2.43)
где B = 
Поскольку
Мx является случайной величиной, в (2.36) необходимо
подставить средний квадрат <| Мx |2>. Воспользовавшись
результатами полученными в [3] запишем
 ,
(2.44) ,
(2.44)
где DDS - дисперсия функции
профиля показателя преломления; rDS (t) - нормированная
корреляционная функция распределения неоднородностей по длине световода DS (r,z).
При радиусе корреляции l0<<l
 , (2.45) , (2.45)
где GDS (0) - спектральная
плотность распределения неоднородностей по длине световода, определяемая
соотношением :
 (2.46) (2.46)
Поскольку
аргумент спектральной плотности должен быть равен нулю, находим величину угла,
под которым в среднем происходит излучение
 (2.47) (2.47)
Полная
средняя излученная мощность будет равна
 (2.48) (2.48)
Таким
образом, мы получили выражение для нахождения характеристик излученной мощности
по известным статистическим характеристикам функций профиля показателя
преломления, определяющих трубчатый источник тока DDS и
GDS (0) или rDS (t).
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50