Студентам > Курсовые > Моделирование распределения потенциала в МДП-структуре
Моделирование распределения потенциала в МДП-структуреСтраница: 1/4
ОГЛАВЛЕНИЕ
МАТЕМАТИЧЕСКАЯ
МОДЕЛЬ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА В МДП-СТРУКТУРЕ
Математическая
модель - - - - - - - - - - - - - - - - - - - 3
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ К
РЕШЕНИЮ ЗАДАЧИ
Использование разностных схем для решения
уравнения Пуассона и для граничных условий
раздела сред
Уравнение
Пуассона - - - - - - - - - - - - - - - - - -
- - - - 5
Граничные условия раздела сред - - -
- - - - - - - - - - - - - - - - - - - 8
Общий алгоритм численого решения задачи
Метод
установления - - - - - - - - - - - - - - - -
- - - - - - 10
Метод переменных направлений - - - -
- - - - - - - - - - - - - - - - - - 13
Построение разностных схем -
- - - - - - - - - - - - - - - - - - - - - 16
ПРИЛОЖЕНИЕ - - - -
- - - - - - - - - - - - - - -
ЛИТЕРАТУРА - -
- - - - - - - - - - - - - - - - -
Математическая модель
распределения потенциала в МДП-структуре
Математическая
модель
Пусть j(x,y) - функция, описывающая
распределение потенциала в полупроводниковой структуре. В области оксла (СDEF) она удовлетворяет
уравнению Лапласа:
d2j + d2j = 0
dx2
dy2
а в области
полупроводника (прямоугольник ABGH) - уравнению Пуассона:
d2j + d2j = 0
dx2
dy2
где
q -
элементарный заряд e;
enn -диэлектрическая
проницаемость кремния;
Nd(x,y) -распределение
концентрации донорской примеси в подложке ;
Na(x,y) -распределение
концентрации акцепторной примеси в подложке;
e0
-диэлектрическая постоянная
На контактах прибора
задано условие Дирихле:
j| BC = Uu
j| DE = Uз
j| FG = Uc
j| AH = Un
На боковых сторонах
полупроводниковой структуры требуется выполнение
однородного условия
Неймана вытекающее из симметричности структуры
относительно линий
лежащих на отрезках AB и GH:
dj = 0 dj = 0
dy AB
dy GH
На боковых сторонах
окисла так же задается однородное условие Неймана
означающее что в
направлении оси OY отсутствует
течение электрического
тока:
dj = 0 dj = 0
dy DC
dy EF
На границе раздела
структуры окисел- полупроводник ставится условие
сопряжения :
j| -0
= j| +0
eok Ex |-0
- enn Ex |+0
= - Qss
где Qss
-плотность поверхностного заряда;
eok -диэлектрическая
проницаемость окисла кремния;
enn -диэлектрическая
проницаемость полупроводника .
Под символом “+0” и”-0” понимают что значение
функции берется бесконечно
близко к границе CF
со стороны либо полупроводника либо
окисла кремния . Здесь
первое условие означает непрерывность потенциала при переходе границы раздела сред а
второе - указывает соотношение связывающее величину разрыва вектора
напряженности при
переходе из одной среды в другую с величиной поверхностного заряда на границе
раздела.
ПРИМЕНЕНИЕ
МАТЕМАТИЧЕСКИХ МЕТОДОВ К
РЕШЕНИЮ ЗАДАЧИ
Использование разностных
схем для решения уравнения Пуассона и для граничных условий раздела сред
Уравнение Пуассона
В области {(x,y)
: 0 < x < Lx , 0 < y
< Ly }
вводится сетка
W={(x,y) : 0
< i < M1 , 0 < j < M2}
x0
=0 , y0=0, xM1 = Lx
, yM2 = Ly
xi+1
= xi + hi+1 , yj+1 = yj+
rj+1
i = 0,...,M1-1
j =
0,...,M2-1
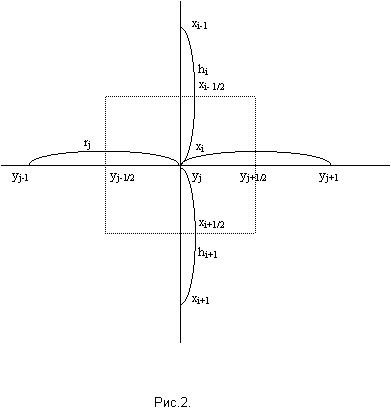
Потоковые точки:
xi+
½ = xi + hi+1
, i = 0,1,...,M1-1
2
yj+
½ = yj + rj+1
, j = 0,1,...,M2-1
2
Обозначим :
U(xi,yj)
= Uij
I(xi+½,yj)
= Ii+½,j
I(xi,yj+½)
= Ii,j+½
Проинтегрируем уравнение
Пуассона:
Dj = - q (Nd + Na)
 e0en e0en
Q(x,y)
по области:
Vij = { (x,y) :
xi- ½ < x < xi+
½ , yj- ½ < y < yj+
½ }
xi+
½ yj+ ½ xi+
½ yj+
½
ò ò Dj dxdy = ò ò Q(x,y)dxdy
xi-
½ yj- ½ xi-
½ yj-
½
Отсюда:
yj+½ xi+½
ò(Ex(xi+½,y)
- Ex(xi-½,y) )dx + ò(Ey(x,yj+½) -
Ey(x,yj-½))dy=
yj-½ xi-½
xi+
½ yj+
½
= ò ò Q(x,y)dxdy
xi- ½ yj-
½
Здесь:
Ex(x,y)
= - dj(x,y)
dx (*)
Ey(x,y)
= - dj(x,y)
dy
x у-компоненты вектора
напряженности электрического поля Е.
Предположим при
yj-½ < y < yj-
½ Ex(xi + ½,yj)
= Ei+ ½ ,j = const
yj-½ < y < yj-
½ Ex(xi - ½ ,yj) = Ei-
½ ,j = const (**)
xi-½ < x < xi+
½ Ey(xi, yj +
½) = Ei,j+ ½ = const
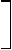 xi-½ < x < xi+
½ Ey(xi, yj -½ ) = Ei,j - ½ = const xi-½ < x < xi+
½ Ey(xi, yj -½ ) = Ei,j - ½ = const
xi-
½ < x < xi+
½
yj-
½ < y < yj+
½ - Q(x,y) = Qij
= const
Тогда
(Ex)i+
½ ,j - (Ex)i -½ ,j r*j
+ (Ey)ij+ ½ - (Ey)ij- ½ h*i
= Qijh*i r*j
где h*i
= hi - hi+1 , r*j = rj
- rj+1
2 2
Теперь Еi+ ½ ,j выражаем через значение j(x,y) в узлах сетки:
xi+1
òEx(x,yj)dx
= - ji+1,j - jij
xi
из (**) при y=yj:
(Ex)i+
½ ,j = - ji+1j - jij
hi+1
Анологично :
(Ey)i,j+
½= - jij+1 - jij
rj+1
Отсюда:
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50