Студентам > Курсовые > Анализ фильтра низких частот
Анализ фильтра низких частотСтраница: 1/2
Введение
Сложность современных объектов, содержащих
сотни тысяч, а порой и миллионы компонентов, делает их проектирование
традиционными (ручными) методами с обязательным изготовлением макета
практически невозможным.
Именно
по этой причине резко возрос интерес разработчиков электронной аппаратуры к
автоматизированным системам проектирования (САПР) и входящим в их состав
подсистемам моделирования.
Математическое моделирование устройств промышленной
электроники проводится как альтернатива физическому моделированию с целью
уменьшения производственных затрат, либо с целью оптимизации параметров разработанных
схем. Задача оптимизации параметров, как правило, отличается большой сложностью
и требует для своего решения значительных затрат машинного времени. Поэтому
эффективность разрабатываемых программ имеет существенное значение и
определяется выбором математической модели устройства, а также методов её
анализа и оптимизации.
В последние годы даже самые консервативно
настроенные разработчики аппаратуры вынуждены пересмотреть свое критическое
отношение к САПР, обнаружив в них весьма мощные и эффективные инструментальные
средства. Особенно привлекательной выглядит возможность, наконец-то, заменить
действующий макет имитационной моделью, а натурные эксперименты - модельными.
Раньше их останавливала недостаточная достоверность имитационных экспериментов,
но теперь, кажется, с этим все в порядке.
САПР
умеют сейчас очень многое. Они позволяют проверять не только правильность
работы проектируемого устройства, но и выяснять его основные характеристики,
начиная с самых первых шагов, когда прорабатываются только архитектурные
решения будущего проекта.
1 Теоретическая
часть
В
данной работе предлагается исследовать характеристики фильтра низких частот,
принципиальная схема которого представлена в приложении А.
В
таблице 1 указаны параметры элементов схемы.
Таблица 1 - Значения номиналов элементов схемы
|
Элемент
схемы
|
Номинальное
значение / название ИС
|
|
С1 |
0,005 мкФ
|
|
С2 |
1 мкФ
|
|
С3 |
0,01 мкФ
|
|
R1
|
120 кОм
|
|
R2
|
100 кОм
|
|
R3
|
20 кОм
|
|
R4
|
120 кОм
|
|
R5
|
10 кОм
|
|
DA1
|
140УД7
|
Данная схема является активным фильтром низких
частот на основе операционного усилителя (ОУ). Применение последнего позволяет
наиболее просто реализовать четыре типа фильтров (верхних и нижних частот,
полосового и заграждающего) - без использования громоздких индуктивностей;
стабилизировать характеристики фильтра, упростить согласование с нагрузкой.
1.1
Фильтры низких частот
В
электрических, радиотехнических и телемеханических установках часто решается
задача: из совокупного сигнала, занимающего широкую полосу частот, выделить
один или несколько составляющих сигналов с более узкой полосой. Сигналы
заданной полосы выделяют при помощи частотных электрических фильтров.
К частотным
электрическим фильтрам различной аппаратуры предъявляются разные, порой
противоречивые требования. В одной области частот, которая называется полосой
пропускания, сигналы не должны ослабляться, а в другой, называемой полосой
задерживания, ослабление сигналов не должно быть меньше определенного значения.
Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление
сигналов и фазо-частотная характеристика линейна (нет искажения формы
сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.
Так как добиться
идеального разделения полосы пропускания и полосы задерживания сигнала
невозможно, говорят об области спада характеристики фильтра.
Исследуемая схема
относится к активным RC-фильтрам. Активными
RC-фильтрами
называют схемы, обладающие способностью изменять спектр сигнала и построенные с
применением только резисторов, конденсаторов и усилительных активных элементов,
при этом индуктивности, широко используемые в обычных электрических
RLC-фильтрах,
имитируются с помощью активных RC-схем, моделирующих индуктивный тип проводимости.
В зависимости от
диапазона частот, относящихся к полосе пропускания, различают низкочастотные,
высокочастотные, полосовые, полосно-подавляющие, избирательные (селективные) и
заграждающие (режекторные) фильтры. Свойства линейных фильтров могут быть
описаны передаточной функцией, которая равна отношению изображений по Лапласу
выходного и входного сигналов фильтра.
Фильтр низких частот - это частотно-чувствительная
схема, которая пропускает некоторый диапазон частот до определенной частоты 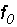 . .
Все
другие частоты выше полосы пропускания значительно подавляются.
Основной
характеристикой фильтров и, в частности, фильтров низких частот, является
амплитудно-частотная характеристика (АЧХ) или ЛАЧХ - логарифмическая
амплитудно-частотная характеристика.
Наряду
с ЛАЧХ или АЧХ фильтра почти всегда приходится исследовать его фазо-частотную
характеристику, а во многих случаях - и переходную характеристику при
импульсных воздействиях.
Типичная АЧХ фильтра
низких частот изображена на рисунке 1.
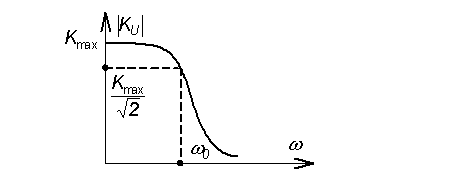
Рисунок 1 - АЧХ ФНЧ
1.2 Математическая
модель операционного усилителя
Задачи математического моделирования подразумевают
формирование схемы замещения исходной схемы, которая содержала бы только базовые
двухполюсники, для которых известны зависимости параметров электрического тока.
Для
того, чтобы составить схему замещения электронной схемы, нужно объединить в
одну систему схемы замещения каждого из элементов исходной схемы.
В
нашем случае базовым двухполюсником не является только операционный усилитель
140УД7. Рассмотрим принципы формирования схемы замещения операционного
усилителя (ОУ).
Схема
замещения операционного усилителя представляет собой схему, содержащую базовые
двухполюсники и отражающую следующие свойства реального ОУ:
- входные свойства (дифференциальные и синфазные
входные сопротивления; входные (разностные) токи);
- усилительные свойства (статический коэффициент
передачи по напряжению; частотно-зависимые и нелинейные свойства коэффициента
передачи: полюса АЧХ, ограничения скорости нарастания выходного напряжения));
-
выходные свойства (выходные сопротивления и ограничения выходного напряжения).
Схема
замещения строится по блочному принципу. На рисунке 2 представлена ее
обобщенная структура.
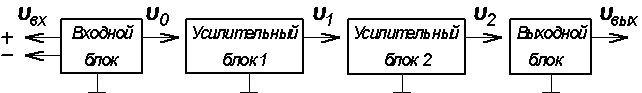
Рисунок
2 - Обобщенная структура схемы замещения ОУ
В
зависимости от того, для исследования каких свойств предназначена схема
замещения ОУ, применяются несколько усилительных блоков.
Коэффициент
передачи рассчитывается следующим образом:
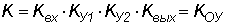
Здесь 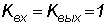 . .
Тогда 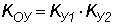 . .
Нам
понадобятся модели ОУ для анализа частотных и временных свойств.
1.2.1
Линеаризованная динамическая модель ОУ
Линеаризованная
динамическая модель ОУ применяется для исследования частотных характеристик. В
общем виде схему замещения ОУ для этого случая можно представить, как это
показано на рисунке 3.

Рисунок
3 - Линеаризованная динамическая схема замещения ОУ
Входной
блок состоит из дифференциального и синфазных входных сопротивлений 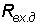 , , 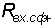 и и 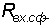 . Входное сопротивление ( . Входное сопротивление (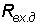 ) - сопротивление
одного из входов ОУ, в то время как другой вход закорочен. Это сопротивление
также называют входным сопротивлением для дифференциального сигнала. Входные
сопротивления для синфазного сигнала ( ) - сопротивление
одного из входов ОУ, в то время как другой вход закорочен. Это сопротивление
также называют входным сопротивлением для дифференциального сигнала. Входные
сопротивления для синфазного сигнала (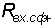 и и 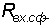 ) - величина их равна отношению приращения
синфазного входного напряжения к приращению среднего входного тока ОУ. Обычно ) - величина их равна отношению приращения
синфазного входного напряжения к приращению среднего входного тока ОУ. Обычно 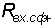 = =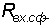 . Значения всех этих параметров
являются справочными данными. . Значения всех этих параметров
являются справочными данными.
Усилительный
блок 1, состоящий из элементов J1, R1, C1,
определяет один полюс и часть коэффициента усиления ОУ.
Здесь 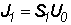 .
(1.1) .
(1.1)
Коэффициент
передачи блока определяется следующим образом:
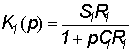 . .
Неизвестными
параметрами являются S1, R1, C1. Для их
определения необходимо назначить коэффициент передачи по напряжению 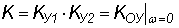 . Также необходимо
задаться одним из параметров (обычно это R1). . Также необходимо
задаться одним из параметров (обычно это R1).
Тогда
искомые значения определяют из следующей системы
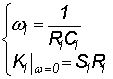 .
(1.2) .
(1.2)
Усилительный
блок 2, состоящий из элементов J2, R2, C2,
моделирует второй полюс. Блок формируется аналогично усилительному блоку 1.
Тогда, на основании (1.1) и (1.2), можно записать
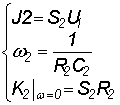 .
(1.3) .
(1.3)
Выходной
блок, состоящий из элементов J3, R3, не отражает
частотных свойств, и для его определения используются следующие выражения
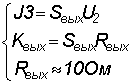 .
(1.4) .
(1.4)
1.2.2 Нелинейная
малосигнальная динамическая модель ОУ
Нелинейная
динамическая модель ОУ для малого сигнала применяется для исследования временных
характеристик схемы.
При
больших входных сигналах и большой емкостной нагрузке p-n-переходы
транзисторов ОУ не успевают перераспределять заряды в соответствии с указанными
полюсами. Данное свойство моделируется в усилительном блоке 1 путем введения
нелинейности в характеристику управляющего источника тока, как это показано на
рисунке 4.

Рисунок
4 - Моделирование скорости нарастания выходного напряжения
а) схема усилительного блока 1;
б) ВАХ нелинейного источника тока
Пусть V - скорость нарастания выходного напряжения. 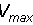 - справочный параметр. - справочный параметр.
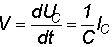 . Если ограничить ток
заряда, мы ограничим скорость заряда. Таким образом . Если ограничить ток
заряда, мы ограничим скорость заряда. Таким образом
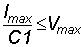 .
(1.5) .
(1.5)
Таким
образом, при формировании усилительного блока 1 появляется необходимость выбора
параметра 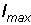 .
Выбор данного параметра возможен на основании выражения (1.5) с учетом того,
что С1 выбрано ранее из соотношения (1.2). Тогда .
Выбор данного параметра возможен на основании выражения (1.5) с учетом того,
что С1 выбрано ранее из соотношения (1.2). Тогда
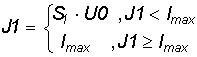 .
(1.6) .
(1.6)
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50